In my last blog post, I introduced the way in which hydrostatic level measurement works. The hydrostatic pressure is used to determine the level through the measurement of the liquid column and is directly proportional to the filling height, as well as to the density of the medium and the force of gravity. Now, how does one calculate, from the hydrostatic pressure, the filling height of an open vessel or an open body of water or well?
Calculation of the filling height using hydrostatic pressure
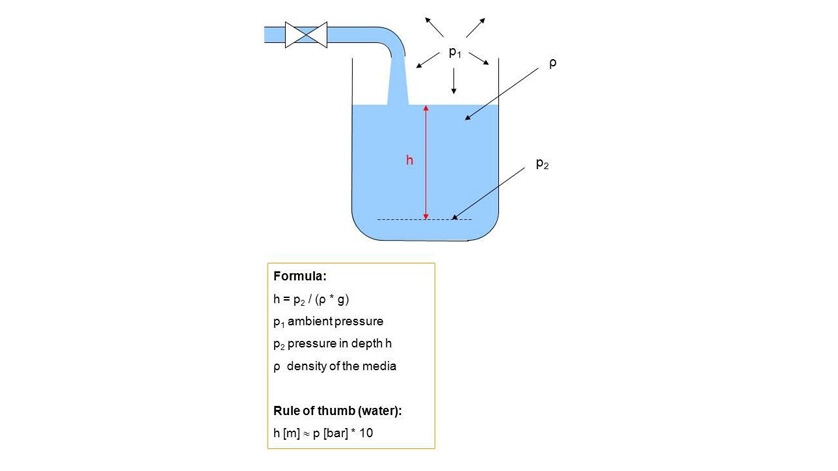
Under the influence of gravity, the hydrostatic pressure rises with the increasing height of the liquid column, thus with the filling height of the vessel.
Thus the level is calculated from the formula:
h = p / (ρ * g)
- p = hydrostatic pressure [bar gauge]
- ρ = density of the liquid [kg/m³]
- g = gravitational force or gravitational acceleration [m/s²]
- h = height of the liquid column [m]
Rule of thumb – Water: h = 1 bar relative / (1000 kg/m³ * ~ 10 m/s²) = 10 m
For the medium water, one can thus adopt the rule of thumb that a pressure of 1 bar corresponds to a filling height of 10 m.
This rule of thumb can be used for selection and specification of a suitable submersible pressure sensor or pressure sensor. As a control, however, a more precise calculation should be performed, which includes the influence of temperature on the density, as well as the location-dependent force of gravity in the level calculation.
Since the density of a medium can significantly deviate from the density of water, this rule of thumb only applies to liquids with densities close to water. Thus, for example, with the same filling height of diesel and water, the hydrostatic pressure of diesel is much lower than that of water.
Example – Diesel fuel: h = 0.82 bar gauge / (820 kg/m³ * ~ 10 m/s²) = 10 m
The density difference has, in this example, led to a measuring error of around 22 %.
Since with hydrostatic level measurement in open basins and vessels, there is constant ventilation, that is to say, a pressure equalisation takes place between the gas above the liquid and the ambient air, the pressure of the overlying gas must not be included in the calculation of the level. By using submersible pressure sensors, such as the WIKA model LH-20, in a gauge pressure variant, the fluctuating ambient pressure is fully compensated.
In my next blog post, I will therefore explain the calculation of the filling height in closed geometries or vessels, and clarify the effect of the enclosed gas on the level measurement.
Note
WIKA offers different solutions for the hydrostatic pressure measurement of level. Our field service will assist you in selecting the suitable pressure sensor for your application.
For more information about this topic, see our information platform “Hydrostatic level measurement”