With hydrostatic level measurement, temperature fluctuations in the medium have an effect on the accuracy of the measurement result. But why is that, and how can you minimise the influence of temperature on hydrostatic level measurement?
In the blog post “Hydrostatic level measurement in open geometries and vessels” the calculation of the filling height is explained in greater detail. Hydrostatic level measurement is not dependent upon the shape of the vessel, and can be calculated with the formula h = p / (ρ * g).
h: Filling height
p: Hydrostatic pressure
ρ: Medium density
g: Gravity
m: Mass
V: Volume
However, the medium density (ρ = m / V) is subject to the influence of temperature. The basis for this is the physical law that a volume expands when the temperature increases under constant pressure. This means that with rising temperature the density of the medium reduces and vice versa. Since the hydrostatic pressure p in open vessels remains constant, the influence of the temperature has a negative effect on the measurement result. Therefore, the measured hydrostatic pressure of a liquid should always be correlated to the medium temperature.
Case example: Deviations in accuracy without temperature compensation
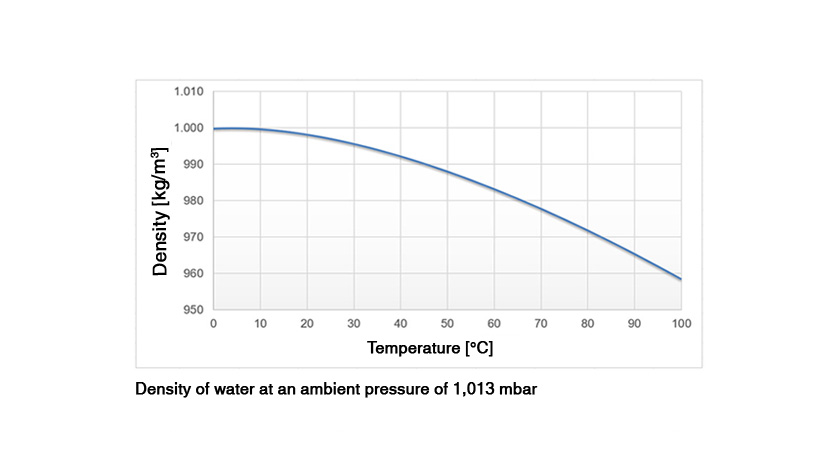
The density of water at room temperature (20 °C) is 998.20 kg/m³. If the same density value is now assumed for the calculation with warm water at 80 °C, then there is a measuring error of 2.7 %, since the density of warm water at 80 °C is only 971.79 kg/m³ (see main picture). For oils and fuels, the temperature-related density change is even greater and thus a measuring deviation of approx. 4.5 % is to be expected for the same example using motor oil.
If you only want to monitor the fill level, while the accuracy plays a subordinate role, a temperature compensation by correcting for the density (see main picture) is not necessary. This is also not required if either no or only small temperature fluctuations prevail in the process. If, however, a precise hydrostatic level measurement with fluctuating medium temperatures is needed, then a compensation for the temperature-related density change is absolutely required. With the knowledge of the current medium temperature, the actual density can be used to calculate the filling height. A temperature-related measuring error is thus prevented.
Note
As a leading manufacturer of hydrostatic level sensors, WIKA offers a large selection of submersible pressure sensors, also featuring integrated temperature measurement. Your contact person will be pleased to advise you on the selection of the appropriate product solution.

